茄子は焼き茄子派です。

みなさま　こんにちは、

通信制高校サポート校のトライ式高等学院徳島キャンパスです！

今回は生徒企画ブログ後編！

前回に引き続き、S君が記事を作成してくれました！

ではS君、どうぞ！！！

交代しましたSです！！

今回！こそは！相対性理論の本論に行きたいと思います！！

「ではさっそく行きましょう！」と言いたいところですが、

前回から1週間も空いてしまったので、軽く復習から行きたいと思います！

前回書かせてもらったことは

・相対性理論は二種類ある

・解説するのに使うのは三平方の定理とみはじの関係のみ

といったことです！

そして最後に、『この世界にはたくさんの原理がある』と言いました。

今回は、たくさんある原理の中で２つ解説するのと共に、

その原理を認めるとどうなるのか←ここ大事

について話していきます！

それでは気を取り直して、行ってみましょう！！

まずは、『光速度不変の原理』について解説していきます！

この原理をめちゃくちゃ簡単に説明すると

「光ってマジ早え！！誰も追いつけねぇ！！」

です。

もう少し詳しく説明すると

『どの慣性系から見ても光の速さは変わらない』

となります。

『慣性系』を抜き出して説明すると、

『等速直線運動』しているか『止まっている』状態であること。です！

加速はダメです！なぜかは聞かないでください（笑）

つまり、秒速１０万㎞で等速直線運動している人から見ても

止まっている人から見ても

光の速さは同じ

ということを言っています。

難しいと感じた人も大丈夫です！

「光には誰も追いつけない、絶対的なもの」だと思っていてください！！

そして次は、『特殊相対性原理』です！

まずこれは『どの慣性系から見ても物理法則は同じ』

といったことを説明していて、例を用いて話すと

動いている電車があって、その中で上方向にボールを投げても、手に戻ってきます

この事象のことを『特殊相対性原理』といいます。

つまり、

どんな状況でもこの地球上にいれば、物理法則は適応されるよ

と、いうことです。

これら二つの原理を認めると、なんと！

動くものの時間は遅れます！！

…っていきなり言われても訳がわからないですよね…。

でも大丈夫です！

ここからは数式と図も用いて、わかりやすく説明していきます。

まずは条件説明です。

縦長という、少しおかしな電車があったとしましょう。

そしてその電車の天井に光を感知する感知器、床には光を発するライトがあります。

さらにその電車外にA君、の中にB君がいます。

こんな感じですね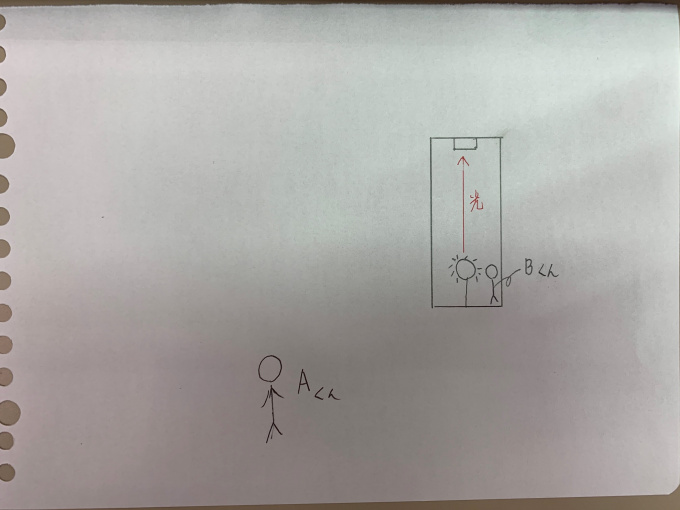

そしてこの電車は、一方向に動くと同時に、ライトから上向きに光が発射されます。

この時、A君から見た光の距離を『TimeA』×『光速度C』でCTA、

同じように、Bから見た光の距離を『TimeB』×『光速度C』でCTBとし、

さらにA君から見た、少し変わった電車が動く距離を『TimeA』×『Velocity(英語で速度という意味)』でVTAとします。

これを図に表すとこうなります。

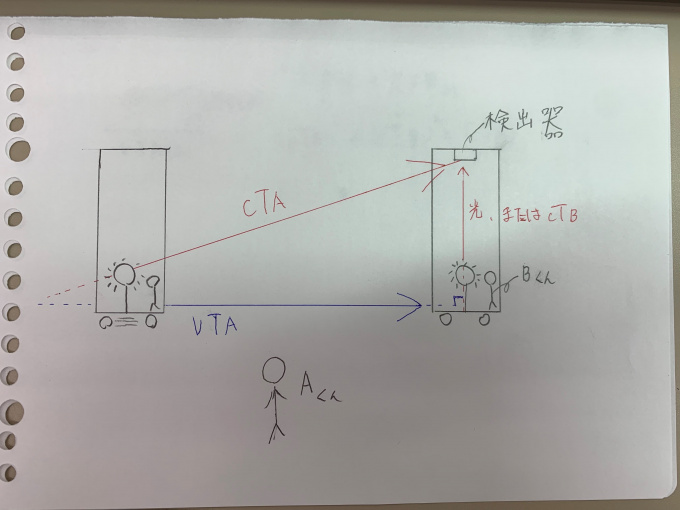
ここから少し難しくなるかもしれません。

ここにできた三角形に、三平方の定理を適応してみましょう。

するとこうなります。

そしてこれを整理した形がこう！！(途中式も書いているのでよかったら見てください！)

さて、ここで出てきた『√１－(V/C)二乗』という式に注目してみたいと思います。

『√１』は『１』で、『√(V/C)二乗』は『V/C』です。

１－(V/C)

は、１からなにかわからないけど、数字を引いているので

１－(V/C)＜１

となります。

これを元々あった式に入れると、

『TB』＝『１より小さい数字』×『TA』

となり、『TA』と『TB』だけを比べると

『TB』より『TA』のほうが大きいことになります。

言葉だけでは何言ってるかわからないと思うので図を用意しました！！

あれ？？『TA』と『TB』って、『TimeA』と『TimeB』でしたよね？？

これが今回の結論で、『動くものの時間は遅れる』ということです！！

どうでしょう、面白くないですか？？

これに限らず相対性理論には、他にも論じていることがあります。

今回は時間でしたが、

今度は長さが縮んだり

１グラムの物体は約９０兆ジュールものエネルギーを保持していたり…

どうですか？『相対性理論』面白いですよね？？

これを機に皆さんが数学や物理を好きになってくれたらうれしいです！

長くなってしまい申し訳ないです……

今度書かせていただく機会があれば、もっと簡潔に、面白く書かせてもらうので

その時は宜しくお願いします！！

では福田さんにお返しします！！

皆さんまた会いましょう！！！！

は～～～い無事返されました、こちら福田です！

S君ありがとう！！！

さ～～～～て

今回の絵しりとりは？？？

卒業生M鈴ちゃん作！

分かるかな～？

トライ式高等学院では随時相談を受け付けております！

フリーダイヤル：0120-919-439